算法概念
K最近邻(k-Nearest Neighbor,KNN)分类算法(这里着重说三次分类、分类、分类),是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:在特征空间中,如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别,则该样本也属于这个类别。
所谓K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例(也就是上面所说的K个邻居), 这K个实例的多数属于某个类,就把该输入实例分类到这个类中。(俗话说:物以类聚人以群分,就是这个道理!)
KNN是机器学习中最简单易懂的算法,它的适用面很广,并且在样本量足够大的情况下准确度很高,多年来得到了很多的关注和研究。
简单示例
举个最简单的示例:
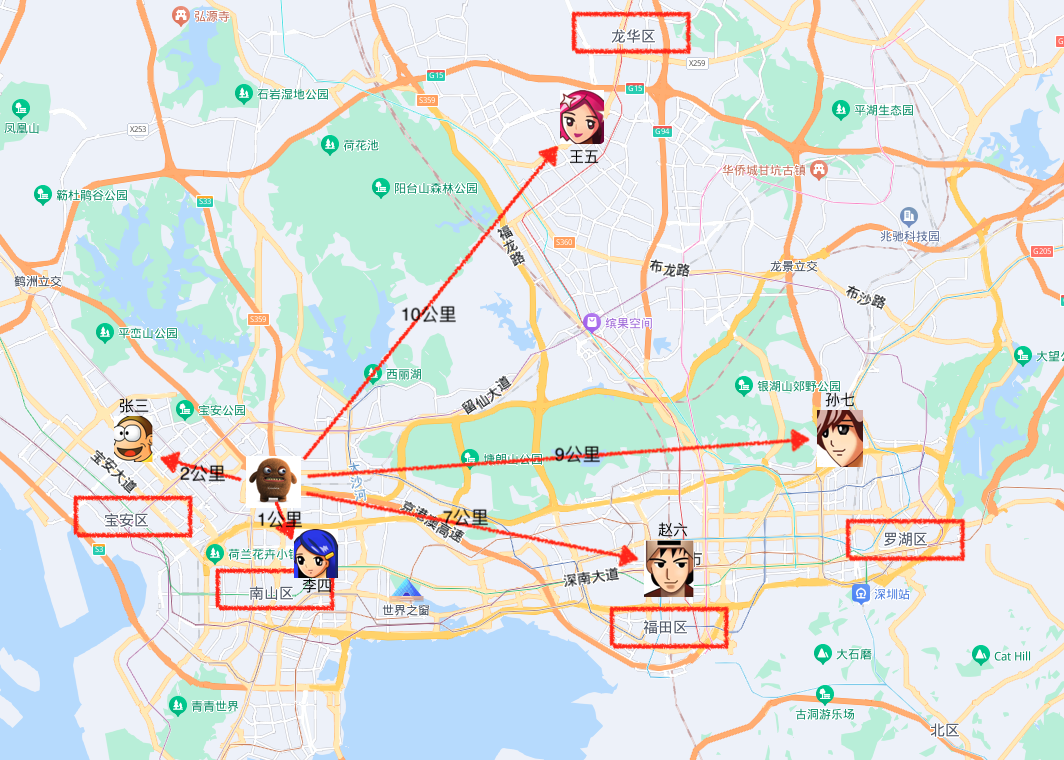
如图所示,小曹刚来深圳入职奇某科技有限公司,现住留仙村路桥洞,同事纷纷好奇的问他留仙村路桥洞属于那个区,小曹也不知道深圳有多少区也不知道留仙村桥洞属于哪个区。但是同事们都知道他们是属于哪个区的,就让小曹在哒哒打车APP上输入每个同事的地址进行计算去往每一个同事家里有多远,选最近的那个同事的距离,就说明小曹住的地方是哪个区的。
从图上的计算路程来看,到李四家1公里路是最近的,李四属于南山区,那留仙村路桥洞就是属于南山区。
如上是样本较少的情况,如果张三附近有一位同事张大嘎子说我是宝安区我去留仙村路桥洞也是1公里路,那么这就不好判断了,也不能说留仙村路桥洞既属于南山区又属于宝安区吧,我们扩大一下范围比如近5公里内所有的同事样本都纳入进来计算,现在我们去公司群里广发英雄贴,让大家把自己的位置和所属区报上来,这样判断也会相对准一些。
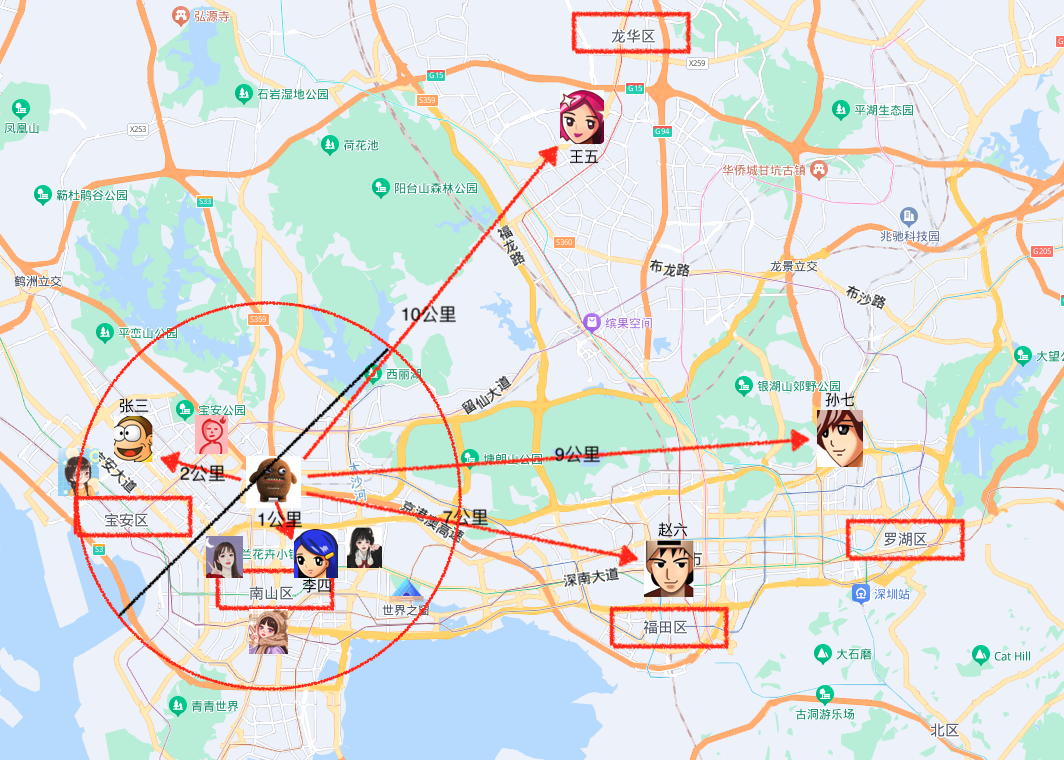
如图上看假设我们选5公里范围内的近邻同事做样本数据,得到的为圈内的人数,通过计算3个在宝安区,4个在南山区,按少数服从多数分类判断为留仙村路桥洞属于南山区。
通过上面的示例再回过头从KNN的算法定义上理解这个K (K个最近样本):
第一张图假设我们定义的K=1,那么从数据上看只找到李四(最近样本就一个),则按李四确定分类=南山区。
第一张图假设我们定义的K=2,那么从数据上看找到了李四、张三(最近样本俩个),则进行分组统计1:1,再按距离最近的是李四,所以做确定分类=南山区。
第一张图假设我们定义的K=3,再加一个样本张大嘎,那么从数据上看找到了张大嘎、李四、张三(最近样本三个),则进行分组统计2:1,分类数2的是宝安区,所以做确定分类=宝安区。
第二张图假设我们定义的K=7,那么从数据上看找到了七个最近样本并进行分组统计4:3,分类数4的是南山区,所以做确定分类=南山区。
第二张图假设我们定义的K=整个样本数,那么整个样本数是10个最近样本,按分类数排序4:3:1:1:1,所以南山区人最多所以做确定分类=南山区。(K取整个样本数则变成哪个分类最多听谁的,假设公司大部分人住罗湖区,那无论你住那都是属于罗湖区,这明显较大偏差,所以K的选择是至关重要)
距离的度量
在上面说到,k近邻算法是在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,我们就说预测点属于哪个类。定义中所说的最邻近是如何度量呢?我们怎么知道谁跟测试点最邻近。这里就会引出我们几种度量俩个点之间距离的标准。但有的人可能就有疑问了,我是要找邻居,找相似性确定分类,怎么又跟距离扯上关系了?
这是因为特征空间中两个实例点的距离可以反应出两个实例点之间的相似性程度。K近邻模型的特征空间一般是n维实数向量空间,使用的距离可以使欧式距离,也是可以是其它距离(曼哈顿距离、切比雪夫距离…),下面我们只介绍欧式距离。
欧氏距离
最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中,如点 x = (x1,…,xn) 和 y = (y1,…,yn) 之间的距离为:
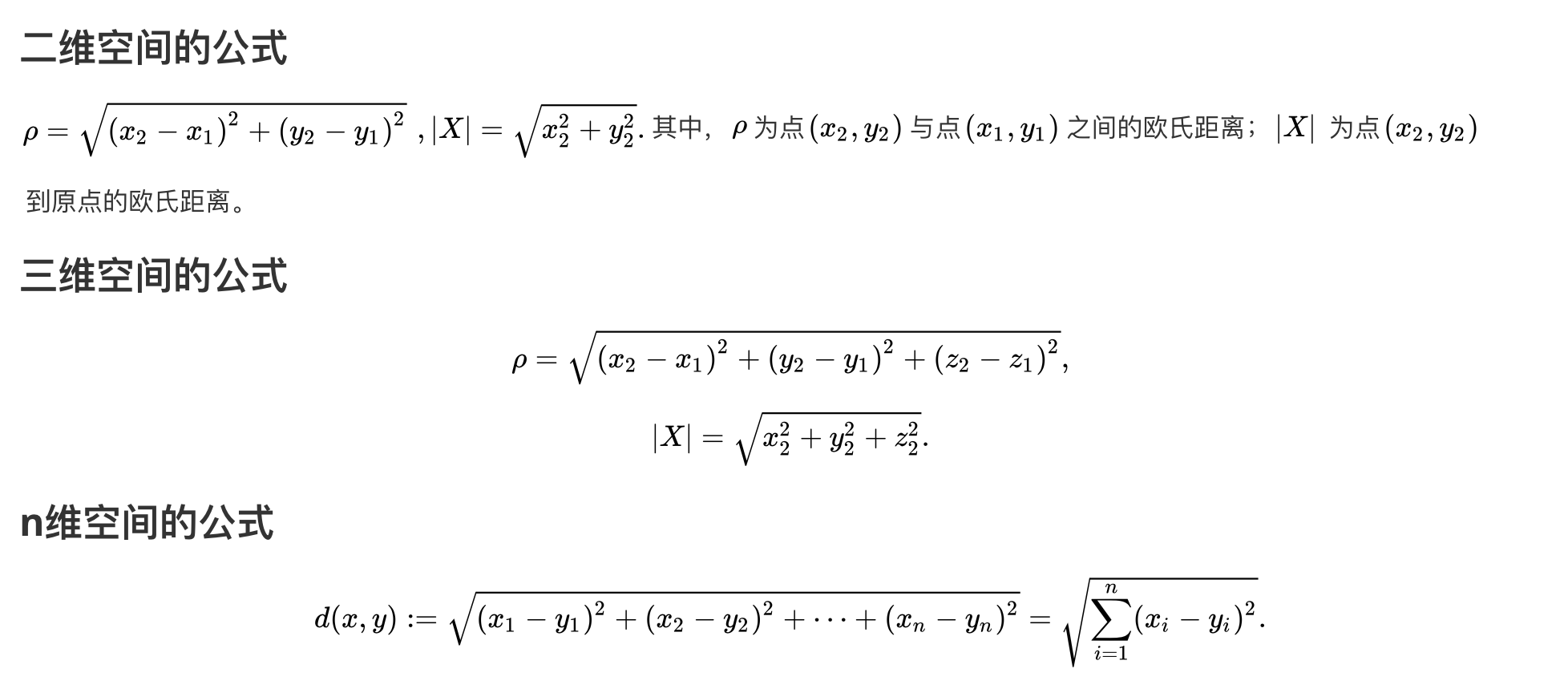
举例
如果上面的公式还不太理解,咱们用下面这个例子去理解关联起来就应该好多了。首先举例如下,我用一个人身高(cm)与脚码(尺码)大小来作为特征值,类别为男性或者女性。我们现在如果有5个训练样本,分布如下:
A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]
现在我来了一个测试样本 F(167,43),让我们来预测他是男性还是女性,我们采取k=3来预测。
下面我们用欧式距离分别算出F离训练样本的欧式距离,然后选取最近的3个,多数类别就是我们最终的结果,计算如下:
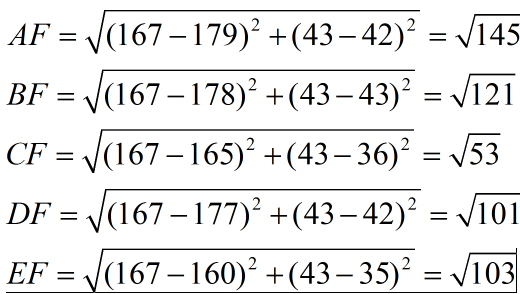
由计算可以得到,最近的前三个分别是C,D,E三个样本,那么由C,E为女性,D为男性,女性多于男性得到我们要预测的结果为女性。
这样问题就来了,一个女性的脚43码的可能性,远远小于男性脚43码的可能性,那么为什么算法还是会预测F为女性呢?那是因为由于各个特征量纲的不同,在这里导致了身高的重要性已经远远大于脚码了,这是不客观的。 所以我们应该让每个特征都是同等重要的!这也是我们要归一化的原因!到这里有人又要问了:什么归一化?
归一化就是把所有数据都转化成[0,1]或者[-1,1]之间的数,其目的是为了取消各维数据之间的数量级差别,避免因为输入输出数据数量级差别大而造成网络预测误差过大。大家看看这个组数据,身高是鞋码的四倍,其实把身高除以4,把数字转变成和鞋码同等状态去做计算对结果反而是个好处,大家可以设想一下如果给的二维样本数据A维值很大、B维值很小,但是B维的值也是起至关重要的作用,但是最后的计算其实A的比率占的极大,大到B维都可以忽略不及的情况,这明显不对的有偏差的。所以我们有必要把这一列的数字进行归一化处理。
归一化公式如下:

最后归一化计算后
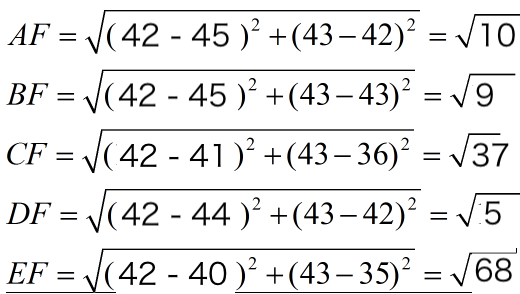
由计算可以得到,最近的前三个分别是A,B,D三个样本,那么由A,B,D全为男性,得到我们要预测的结果为男性。由此可见归一化后准确率极高。
精选示例
有一种兔子叫作 (丧彪),它们的平均身高是 50 厘米,平均体重 55 公斤。我们拿来一百个丧彪,分别测量它们的身高和体重,画在坐标图上,用绿色方块表示。
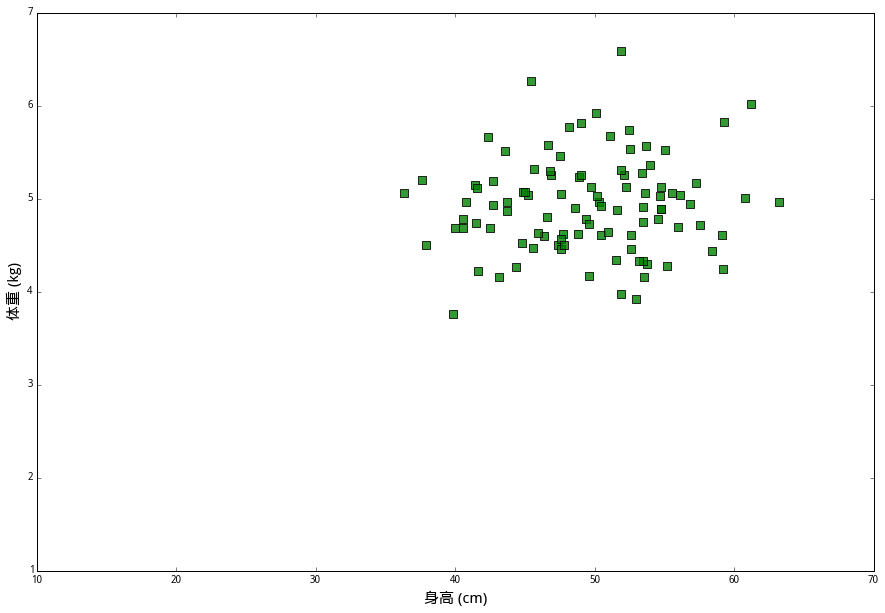
还有一种兔子呢,叫作 (小美)。它们体型比较小,平均身高是 30 厘米,平均体重是 44 公斤。我们将一百个小美的身高和体重画在同一个坐标图上,用蓝色三角表示。
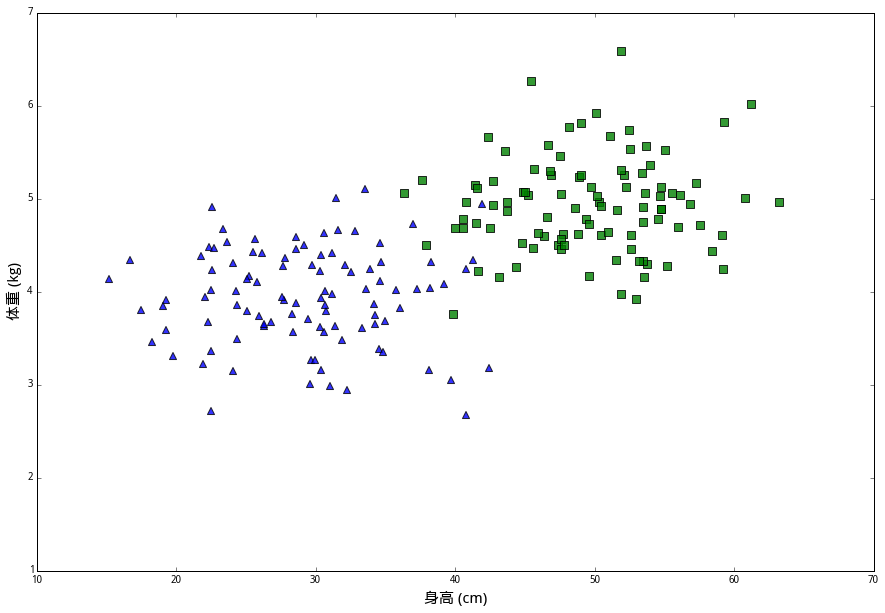
最后一种兔子叫 (大壮)。它们的平均身高45厘米,但体重较轻,平均只有2.5公斤。一百只大壮的数据用黄色圆圈表示。
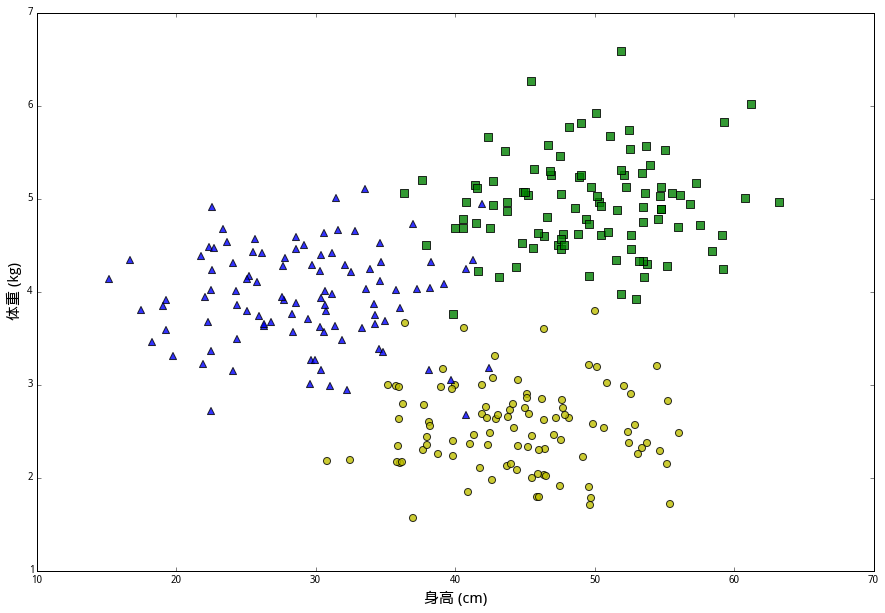
在这些数据中,(身高,体重) 的二元组叫做特征(features),兔子的品种则是分类标签(class label)。我们想解决的问题是,给定一个未知分类的新样本的所有特征,通过已知数据来判断它的类别。
假设梧桐山森林公园里经常出现这三种兔子。为了了解它们的生态环境,奇某科技公司户外野生动物研究组想知道三种兔子的数量比例;可是这些森林又太过危险,不能让人亲自去做,所以要设计一个全自动的机器人,让它自己去森林里识别它遇到的每一个兔子的种类。假设奇某科技公司次团队经费不足,所有机器只有测量兔子的身高和体重的能力。
那么现在有一只奇怪的兔子,我们想判断它的类别,要怎么做呢?按照最普通的直觉,应该在已知数据里找出几个和我们想探究的兔子最相似的几个点,然后看看那些兔子都是什么个情况;如果它们当中大多数都属于某一类别,那么这只奇怪的兔子大概率也就属于该类别了。
于是我们给机器人预设一个K的整数,让它去寻找最近的K个数据样本进行分析,目前机器它只测量出这只兔子身长 37 厘米,体重 4.8 公斤 (经费有限,机器就只有这两个测量技能),就是下面图中那颗闪闪发亮的红星。
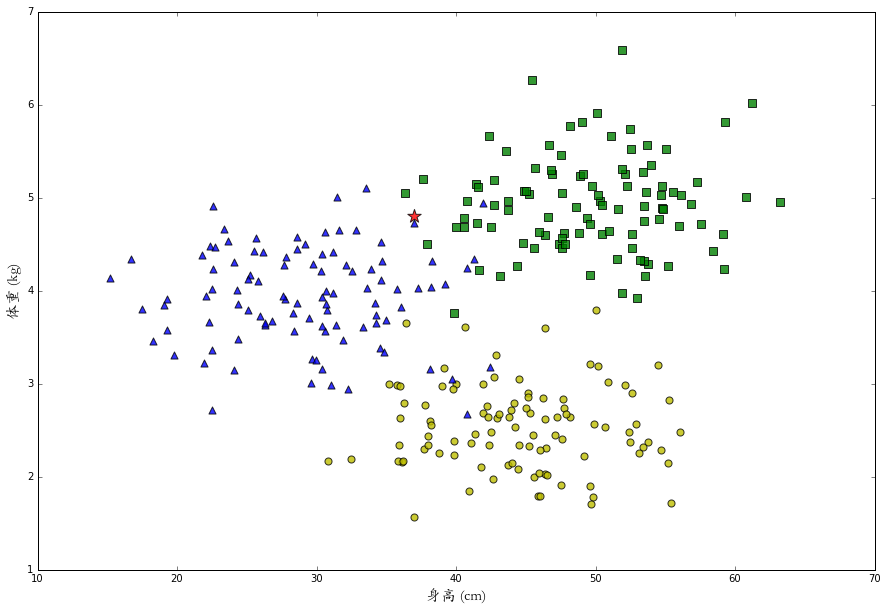
如果设 k=15,算法会判断这只兔子是一只丧彪。但是如果设 k=1,那么由于距离最近的是蓝色三角,会判断这只兔子是一只小美。可是这只兔子的特征数据在丧彪和小美的分界处,机器不论判断它属于哪个类别都很有可能是错的。这时,类似“它有一半可能性是丧彪,一半可能性是小美”的反馈会更有意义。
为了这个目的,我们同样找找出距离问题特征最近的K个样本,但与其寻找数量最多的分类,我们统计其中每个类别的分别有多少个,再除以K得到一个属于每一个类别概率值。比如在上面的图里,距离五角星最近的 1515 个样本中,有 88 只丧彪和 77 只小美,由此判断:它有 53% 的可能性是丧彪,47%的可能性是小美,0%的可能性是大壮。
在整个二维空间中的每一个点上进行概率 KNN 算法,可以得到每个特征点是属于某个类别的概率热力图,图中颜色越深代表概率越大。
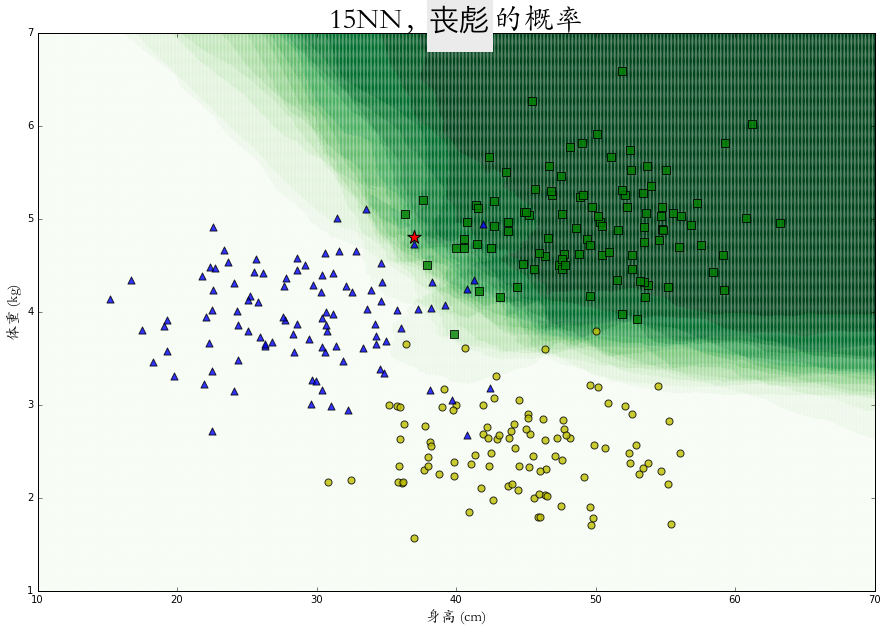
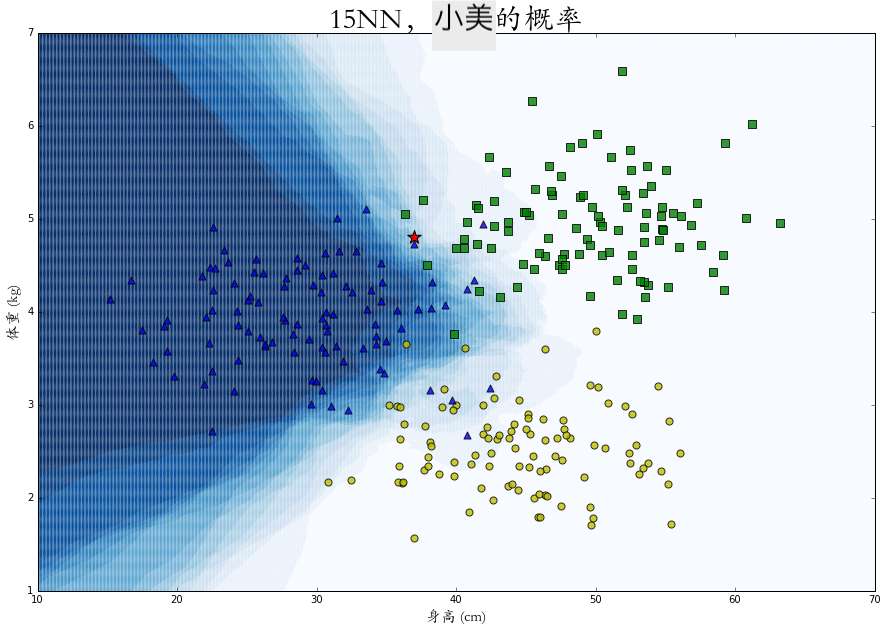
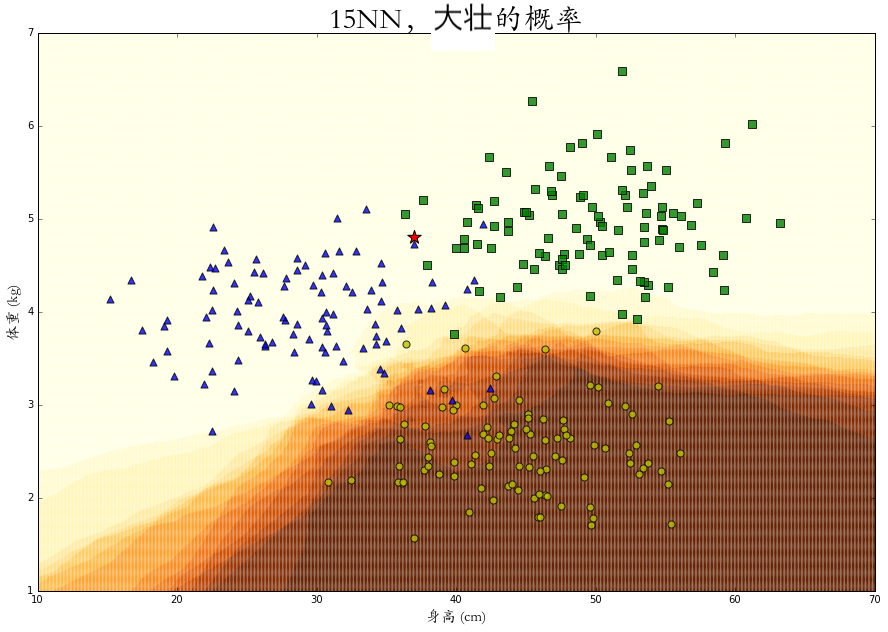
相比于绝对的分类,这些概率的计算会给我们更有效的表述以及更多的应用空间。
再假设我们了解到丧彪这种兔子喜欢到处大小便,尤其是遇到机器人的时候就爱凑近机器人屙一把,工作人员对此也无可奈何。所以我们想让机器人在测量并发现是丧彪之后马上掉头逃跑。但是如果机器发现了一只体型接近丧彪和小美,并且普通的 KNN 算法发生误判,没有马上逃跑,那么最后就会被喷了。所以我们使用概率 KNN 的算法并且使用以下风控原则:只要发现兔子有 30%以上的概率是丧彪,就马上逃跑。从此之后,机器人就再也没被屙臭过。
最后
我们的示例,却丝毫没有提及如何用代码计算 KNN。这是因为 KNN 虽然思路简单,但实现起来有一个问题,那就是计算量很大;当数据量很多时,拿一组特征来和所有样本依次计算距离并选取最近的 K个,是非常耗费时间的。KNN 的一个高效算法—kd树大家有兴趣开源自行了解。
以上给的示例参考了如下文章作者的示例和图(我做了些名称改动):
https://www.joinquant.com/view/community/detail/a98b7021e7391c62f6369207242700b2